图像分割

图像分割基础

• 图像分割算法多数是基于灰度图像的两个基本性质之一：不连续性和相似性。对于不连续的灰度，方法是以灰度突变为基础分割一幅图像，比如图像的边缘。对于相似的灰度，主要方法是根据一组预定义的准则把一幅图像分割为相似的区域，如阈值处理、区域生长、区域分裂和区域聚合。综合运用不同方法改善分割的性能，比如，边缘检测可以结合阈值处理。

• 图像分割：令R表示一幅图像的整个空间区域，把图像分割视为把R分为n个子区域$R_1$、$R_2$…$R_n$的过程，必须满足以下条件：

  1. $\cup_{i=1}^{n}R_i=R$;
  2. $R_i$是一个连通集，$i=1,2,…,n$;
  3. $R_i\cap R_j=\varnothing$，对于所有i和j，$i\neq j$；
  4. $Q(R_i)=TURE，i=1,2,…,n$；
  5. $Q(R_i\cup R_j)=FALSE$，对于任何$R_i$和$R_j$的邻接区域。

  其中，$Q(R_k)$ 是定义在集合$R_k$的点上的一个逻辑属性，比如，如果$R_k$中像素的平均灰度小于$m_i$，且灰度标准差大于 $\sigma_i$，$m_i$和 $\sigma_i$是指定的正常数，则$Q(R_k)=TURE$。

点、线和边缘检测

背景知识

• 一阶和二阶导数边缘检测的特性

  1. 一阶导数通常在图像中产生较粗的边缘；
  2. 二阶导数对精细细节，如线、孤立点和噪声有较强的响应；
  3. 二阶导数在灰度斜坡灰度台阶过渡会产生双边缘响应；
  4. 二阶导数的符号可用于确定边缘的过渡是否从亮到按还是从暗到亮。
• 导数对噪声非常敏感，因此在使用导数进行边缘检测时，应对图像降噪处理。
• 计算机图像中每个像素位置处的一阶导数和二阶导数的计算可以通过空间滤波器。
• 模板中系数和为0，表明恒定灰度区域中的响应为0。以下左侧为常用的拉普拉斯滤波器模板，右侧为带有对角项的扩展模板：

\[\begin{bmatrix} 0 & 1 & 0\\ 1 & 4 & 1\\ 0 & 1 & 0 \end{bmatrix} \quad\quad\quad \begin{bmatrix} 1 & 1 & 1\\ 1 & 8 & 1\\ 1 & 1 & 1 \end{bmatrix}\]

点检测

• 点检测使用如下表达式得到： \(g(x,y)= \begin{cases} 1, & |R(x,y)| \geq T \\ 0, & otherwise \end{cases}\)

线检测

• 线检测使用拉普拉斯模板处理后，必须处理二阶导数的双线效应。

  • 负值可通过去拉普拉斯图像的绝对值简单处理，但结果的线宽会增加；
  • 仅使用拉普拉斯的正直，这种方法会产生更细的线。
  • 零灰度轴和二阶导数极值间的连线的交电，称为二阶导数的 零交叉点。
  • 前述拉普拉斯检测模板是各向同性的，因此其响应与方向无关，如果要检测特定方向的线，则需使用首选方向比其他方向更大的系数加权的模板，以下为对$45^。$有最佳响应的模板： \(\begin{bmatrix} 2 & -1 & -1\\ -1 & 2 & -1\\ -1 & -1 & 2 \end{bmatrix}\)

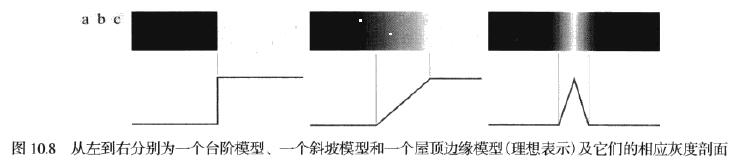
• 边缘模型

  • 台阶模型：在1像素的距离上出现两个灰度级间的理想过渡。坎尼(Canny)边缘检测算法用台阶边缘模型推导。
  • 斜坡模型：灰度级的过渡较台阶模型较平缓。
  • 屋顶模型

• 执行边缘检测的三个基本步骤：

  1. 因为导数对微弱的噪声的敏感性，需对图像进行降噪处理；
  2. 边缘点的检测，这是一个局部操作，从一幅图像中提取所有的点，这些点是变为边缘点的潜在候选者；
  3. 边缘定位，从候选边缘点中选择组成边缘点集合的真实成员。

基本边缘检测

• 图像f在$(x,y)$用梯度表示边缘的强度和方向，梯度 $\nabla f$表示： \(\nabla f = grad(f) = \left[ \begin{array}{c} g_x \\ g_y \end{array} \right] = \left[\begin{array}{c} \frac{\partial f} {\partial x} \\ \frac{\partial f} {\partial y} \end{array} \right]\)

• 梯度的性质：

  • 向量 $\nabla f$的大小表示为$M(x,y)$,即： \(M(x,y)=mag(\nabla f)=\sqrt{g_x^2+g_y^2}\) 因为平方和平方根需要大量的计算开销，经常用绝对值来近似梯度的幅值： \(M(x,y)=|g_x|+|g_y|\)

  • 梯度向量的方向由下列对于x轴度量的角度给出： \(\alpha(x,y)=arctan[\frac{g_y}{g_x}]\) 任意点(x,y)的边缘的方向与该点梯度向量的方向 $\alpha(x,y)$ 正交。

• $g_x$，$g_y$，$M(x,y)$ 和 $\alpha(x,y)$都是与原图像相同的图像。

  梯度算子：

  1. Prewitt算子

\[\begin{bmatrix} -1 & -1 & -1\\ 0 & 0 & 0\\ 1 & 1 & 1 \end{bmatrix} \quad \begin{bmatrix} -1 & 0 & 1\\ -1 & 0 & 1\\ -1 & 0 & 1 \end{bmatrix}\]

1. Sobel算子，在中心位置处使用2可以平滑图像。

\[\begin{bmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1 \end{bmatrix} \quad \begin{bmatrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1 \end{bmatrix}\]

对如下图像执行Sobel算子运算： \(\begin{bmatrix} z_1 & z_2 & z_3\\ z_4 & z_5 & z_6\\ z_7 & z_8 & z_9\\ \end{bmatrix}\) 得到： \(g_x=\frac{\partial f}{\partial x}=(z_7+2z_8+z_9)-(z_1+2z_2+z_3)\) 和 \(g_y=\frac{\partial f}{\partial x}=(z_3+2z_5+z_9)-(z_1+2z_4+z_7)\)

• Prewitt模板实现起来比Sobel模板更为简单，Sobel模板能更好的抑制噪声。
• 如下修改的Prewitt和Soble模板，有沿对角线方向的最大响应： \(\begin{bmatrix} 0 & 1 & 1\\ -1 & 0 & 1\\ -1 & -1 &0 \end{bmatrix} \quad \begin{bmatrix} -1 & -1 & 0\\ -1 & 0 & 1\\ 0 & 1 & 1 \end{bmatrix}\)

\[\begin{bmatrix} 0 & 1 & 2\\ -1 & 0 & 1\\ -2 & -1 & 0 \end{bmatrix} \quad \begin{bmatrix} -2 & -1 & 0\\ -1 & 0 & 1\\ 0 & 1 & 2 \end{bmatrix}\]

• 结合平滑处理和阈值处理，可以得到更理想的结果。

更先进的边缘检测技术

• 通过利用图像特性和噪声内容采取预防措施为基础的边缘检测算法。

Marr-Hildreth边缘检测器

• 边缘检测算子应有的两个明显的特点：

  1. 应能够计算图像中每一点处的一阶导数或二阶导数的数字近似值；
  2. 算子的尺寸可以被调整，以便在任何期望的尺寸上起作用，大尺寸算子可以用于检测模糊边缘，小尺寸算子可用于检测尖锐度集中的精细细节。

• Marr and Hildreth证明满足以上两个条件的算子是滤波器 $\nabla^2G$。 其中

1. $\nabla$是拉普拉斯算子 \(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\)

2. G是标准差为 $\sigma$的二维高斯函数 \(G(x,y)=e^{-\frac{x^2+y^2}{2\sigma^2}}\)

• $\nabla^2G$表达式如下： \(\nabla^2G(x,y)=[\frac{x^2+y^2-2\sigma^2}{\sigma^4}]e^{-\frac{x^2+y^2}{2\sigma^2}}\) 该表达式称为 高斯拉普拉斯(LoG),有时也称为 墨西哥草帽算子。

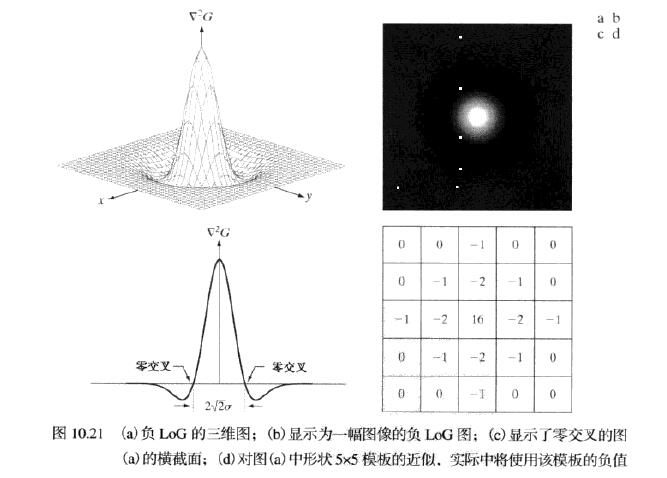
• Marr-Hildreth算子的操作过程：

LoG滤波器与输入图像f(x,y)进行卷积操作： \(g(x,y)=[\nabla^2G(x,y)]\star f(x,y)\) 然后寻找输出图像g(x,y)的零交叉来确定f(x,y)中边缘的位置。因为上述操作是线性操作，所以上式可以如下表达： \(g(x,y)=\nabla^2[G(x,y)\star f(x,y)]\) 表明，可以先用一个高斯滤波器平滑图像，然后计算该结果的拉普拉斯。

Canny边缘检测器

• Canny检测器是迄今讨论过的边缘检测器中最为优秀的，该算法基于以下三个基本目标：

  1. 低错误率，所有边缘都应被找到，并且没有伪响应。
  2. 边缘点应被很好的定位，已定位边缘必须尽可能接近真实边缘。
  3. 单一的边缘点响应，对于真实的边缘点，检测器仅应返回一个点。

• Canny边缘检测算法的基本步骤：

  1. 用一个高斯滤波器平滑输入图像； \(f_s(x,y)=G(x,y) \star f(x,y)\)

  2. 计算梯度幅度值图像和角度图像； \(M(x,y)=mag(\nabla f)=\sqrt{g_x^2+g_y^2}\) \(\alpha(x,y)=arctan[\frac{g_y}{g_x}]\)

  3. 对梯度幅度值图像应用非最大抑制；
     • 寻找最接近 $\alpha(x,y)$ 的方向 $d_k$;
     • 若 $M(x,y)$ 的值至少小于沿 $d_k$的两个邻居之一，则令 $g_N(x,y)=0$(抑制)，否则，令 $g_N(x,y)=M(x,y)$。$g_N(x,y)$ 是非最大抑制后的图像。
  4. 用双阈值处理和连接分析来检测并连接边缘。
     • 低阈值 $T_L$和高阈值 $T_H$的比率应为3:1或2:1。
     • 双阈值处理，$g_{NH}(x,y)$ 和 $g_{NL}(x,y)$ 中的非零像素可分别视为“强”和“弱”边缘像素。 \(g_{NH}(x,y)=g_N(x,y) \geq T_H \\ g_{NL}(x,y)=g_N(x,y) \geq T_L \\ g_{NL}(x,y)=g_{NL}(x,y) - g_{NH}(x,y)\)
     • 连接分析：逐个访问$g_{NH}(x,y)$ 中的非零像素p，使用8连通的连接方式将$g_{NL}(x,y)$ 中所有弱像素标记为有效边缘像素。将$g_{NL}(x,y)$ 中的非有效边缘像素置零。最后将$g_{NL}(x,y)$ 中的所有非零像素添加到$g_{NH}(x,y)$ 中，即得到最终输出图像。

• 各种边缘检测算法的比较：

  1. Canny算法与其他算法相比，得到的图像边缘效果更好；
  2. 比Marr-Hildreth算法、阈值梯度等算法相比，实现更复杂，需要的计算量更大。
  3. 实时工业图像处理时，成本和速度需求通常要求使用更简单的技术，主要是梯度阈值算法；当关注的主要是边缘质量时，通常会使用Marr-Hildreth算法和Canny算法。

边缘连接和边界检测

• 理想情况下，边缘检测仅产生位于边缘上的像素集合。
• 实际上，由与噪声、不均匀照明引起的边缘间断，以及其他引入灰度值虚假的不连续的影响，这些像素并不能完全描述边缘特性。
• 一般是在边缘检测后紧跟连接算法，将边缘像素组合成由意义的边缘区域边界。
• 边缘连接的方法：
  • 局部处理：需要由关局部区域中边缘点的知识
  • 区域处理：要求区域边界上的已知点
  • 处理这个边缘图像的全局方法

    局部处理

    1. 令$S_{xy}$ 表示一幅图像中以点(x,y)为中心的一个邻域的坐标集合，如果： \(|M(s,t)-M(x,y)| \leq E\) 式中E是一个正阈值。

1. 梯度向量的方向满足： \(|\alpha(s,t)-\alpha(x,y)| \leq A\) 式中A是一个正角度阈值。

2. 如果同时满足以上两个条件（幅度和方向），则$S_{xy}$ 中，坐标(s,t)的像素被连接到坐标为(x,y)的像素。
3. 以上3个步骤必须检验每个点的所有邻点，所以计算量很大。在实际中，使用简化的步骤连接。

   区域处理

阈值处理

• 阈值处理更直观、实现简单且计算速度快，因此图像阈值处理在图像分割应用中处于核心地位。
• 一幅图像f(x,y),指定阈值T，得到结果图像g(x,y)的公式： \(g(x,y)= \begin{cases} 1, & \quad f(x,y) > T \\ 0, & \quad f(x,y) \leq T \end{cases}\) 当T是一个适用于整个图像的常数时，上式给出的处理称为 全局阈值处理*；当T值在一幅图像中改变时，称为 可变阈值处理。

  基本全局阈值处理

• 对图像自动估算阈值的算法：
  1. 为全局阈值T选择一个初始估值，通常选用图像的平均灰度；
  2. 利用初始估值T对图像分割，得到两组像素：$G_1$ 由灰度值大于T的所有像素，$G_2$ 由灰度值小于等于T的像素组成；
  3. 对$G_1$和$G_2$分别计算平均灰度值$m_1$和$m_2$；
  4. 计算一个新的阈值： \(T=\frac{1}{2}(m_1+m_2)\)

1. 重复步骤2到4，知道连续迭代中的T值间的差小于一个预定义的参数 $\Delta T$为止。

用Otsu方法的最佳全局阈值处理

1. 计算输入图像的归一化直方图。使用$p_i$，i=0,1,2,…,L-1表示该直方图的各个分量； \(\sum_{i=0}^{L-1}p_i=1, \quad p_i \geq 0\) 其中，$p_i=\frac{n_i}{MN}$，$n_i$表示灰度级为i的像素个数，MN表示总像素个数，L-1表示灰度级的最大值。

2. 利用下式，对于k=0,1,2,…,L-1，计算累积和$P_1(k)$; \(P_1(k)=\sum_{i=0}^{k}p_i\)

3. 利用下式，对于k=0,1,2,…,L-1，计算累积和$m(k)$; \(m(k)=\sum_{i=0}^{k}ip_i\)

4. 利用下式计算整个图像的全局灰度均值； \(m_G=\sum_{i=0}^{L-1}ip_i\)

5. 利用下式，对于k=0,1,2,…,L-1，计算类间方差 $\sigma_B^2(k)$; \(\sigma_B^2(k)=\frac{[M_GP_1(k)-m(k)]}{P_1(k)[1-P_1(k)]}\)

6. 得到Otsu阈值 $k^$ 使得 $\sigma_B^2(k)$ 最大k值，如果最大值不唯一，用相应检测到的各个最大值k的平均得到 $k^$ ；
7. 在$k=k^$ 处计算 $\eta(k)=\frac{\sigma_B^2(k)}{\sigma_G^2}$，得到可分性测度 （$0 \leq \eta(k^) \leq 1$）。

用图像平滑改善全局阈值处理

• 当图像受噪声影响使得直方图峰谷不清，不利于阈值处理，这就需要在阈值处理之前平滑图像，再进行阈值处理，分割图像。
• 当需要分离的部分相对于背景很小，以至于该区域对直方图的贡献与由噪声引起的灰度扩散相比无足轻重，图像平滑的全局阈值处理的效果就不明显，就需要结合图像边缘改进的全局阈值处理。

利用边缘改进全局阈值处理

• 处理步骤：
  1. 对图像f(x,y)使用任意一种边缘检测算法获得图像g(x,y)；
  2. 指定一个阈值T，对g(x,y)进行阈值处理，得到二值图像$g_T(x,y)$；
  3. 对f(x,y)和$g_T(x,y)$ 求积，得到图像 $g_M(x,y)$；
  4. 使用Otsu方法分割图像$g_M(x,y)$，即得到最终分割后的图像。

多阈值处理

可变阈值处理

1. 图像分块
   • 可变阈值处理最简单的方法是把一幅图像分割称不重叠的矩形，使用这种方法用于补偿光照和/反射的不均匀。只要矩形足够小，以便每个矩形的光照都近似是均匀的。
   • 对分割的后的矩形采用前述的阈值处理（如Otsu阈值处理），得到分割图像。
2. 基于局部图像特性的可变阈值处理
3. 使用移动平均

多变量阈值处理

基于区域分割

区域生长

• 基于8邻接的一个基本区域生长算法的执行过程：
  1. 在S(x,y)中寻找所有连通分量，并把每个连通分量腐蚀为一个像素；把找到的所有像素标记为1，把S中的所有其他像素标记为0；
  2. 在坐标对(x,y)处形成图像$f_Q$ :若输入图像在该坐标处满足给定的属性Q，则令$f_Q(x,y)=1$，否则令$f_Q(x,y)=0$；
  3. 令g是这样形成的图像：即把$f_Q$中为8邻接种子点的所有1值点，添加到S中的每个种子点；
  4. 用不同的区域标记（比如1，2，3，…）标出g中的每个连通分量。这就是区域生长得到的分割图像。

其中，f(x,y)表示一个输入图像，S(x,y)表示一个种子阵列，种子点 位置处为1，其他位置处为0；Q表示在每个位置(x,y)处所用的属性。假设f和S的尺寸相同。

区域分裂与聚合

• 将一幅图像细分为任意的不相交区域，然后聚合和/或分裂这些区域。算法的执行过程：
  1. 把满足$Q(R_i)=FALSE$的任何区域$R_i$分裂为4个不相交的象限区域；
  2. 当不能再分裂时，对满足条件$Q(R_i \cup R_j)=TRUE$的任何两个邻接区域$Q(R_i)$ 和$Q(R_j)$ 进行聚合；
  3. 无法进一步聚合时，停止操作，完成图像的分割。

其中R表示整幅图像，$Q(R_i)$ 表示分割后的区域，Q表示某一指定的条件，比如图像灰度的平均值m，标准差$\sigma$满足指定要求。

• 一般会设定一个无法进一步执行分裂的最小四象限的尺寸。

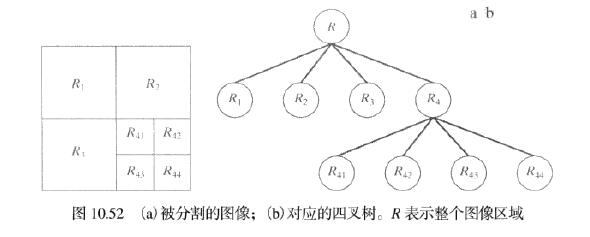
用形态学分水岭的分割

• 以三维的方式形象化一幅图像，将图像划分为不同的由分水岭划分的汇水盆地。通过向图像中不同区域的灰度最小值位置向上注水，通过构造水坝防止水由一个汇水盆地越过分水岭时进入另一个汇水盆地，这些构造的水坝可以将图像分割。
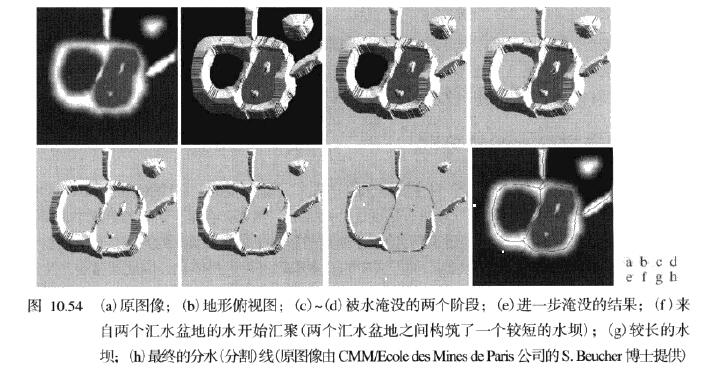
• 分水岭分割主要应用之一是，从背景中提取近乎一致（类似水滴）的物体。由较小的灰度表征的区域有较小的梯度值，因此，常常用分水岭分割方法分割一幅图像的梯度。

分割中运动的应用

• 运动来自感觉系统和正被观看场景间的相对位移。

  差值图像

• 差值图像（$d_{ij}(x,y)$）是通过选取视频中$t_i$和$t_j$时刻的两帧图像，进行如下计算获得： \(d_{ij}(x,y)= \begin{cases} 1,& \quad |f(x,y,t_i)-f(x,y,t_j)|>T\\ 0,& \quad otherwise \end{cases}\) 表明将图像中的固定成分置零，非固定成分（运动成分）灰度值设置为1。

累积差值图像（ADI）

• 对于一个图像帧序列$f(x,y,t_1),f(x,y,t_2),…,f(x,y,t_n)$，令$f(x,y,t_1)$ 为参考图像，通过以下函数计算绝对ADI，正ADI和负ADI。
  1. 绝对ADI \(A_k(x,y)= \begin{cases} A_{k-1}(x,y)+1,& \quad |R(x,y)-f(x,y,k)|>T \\ A_{k-1}(x,y), & \quad otherwise \end{cases}\)

1. 正ADI \(P_k(x,y)= \begin{cases} P_{k-1}(x,y)+1,& \quad R(x,y)-f(x,y,k)>T \\ P_{k-1}(x,y), & \quad otherwise \end{cases}\)

2. 负ADI \(N_k(x,y)= \begin{cases} N_{k-1}(x,y)+1,& \quad R(x,y)-f(x,y,k)<-T \\ N_{k-1}(x,y), & \quad otherwise \end{cases}\) 其中$R(x,y)=f(x,y,t_1)$，表示参考图像。$k=t_k$。以上三式的前提是运动物体的灰度值大于背景，如果相反，则正ADI和负ADI的计算中不等式的顺序和阈值符号是与上式相反。

• 参考图像的建立：选取图像帧序列的两幅图像可以得到固定元素，获得参考图像的更一般的做法是，选取一组包含一个或多个运动物体的图像，当一个非固定成分完全一处参考帧的位置时，当前帧中对应的背景可复制到最初被参考帧中物体占据的位置。

其他

• 超像素(superpixel):把图像分割为灰度、质地、结构等相同的多组像素集合；超像素具有处理更高效、更有意义的表达效果等特点。通常使用Normalized Cuts algorithm过分割（oversegmetation）图像得到。 Superpixel: Empirical Studies and Applications

• placeholder